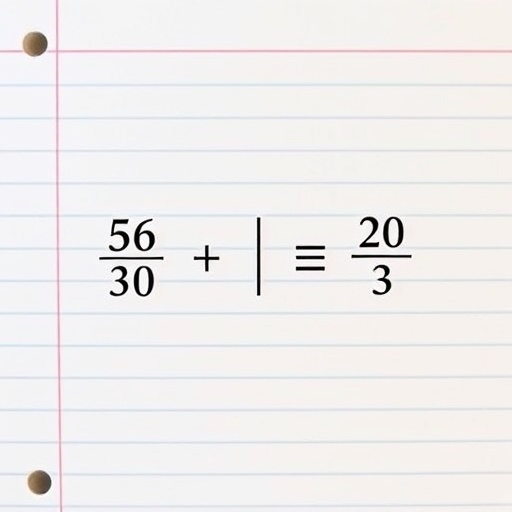Os números racionais são fundamentais no estudo da matemática, representando quantidades que podem ser expressas como frações, onde um número inteiro é dividido por outro não nulo. Eles englobam os números inteiros, as frações positivas e negativas, além dos decimais finitos e periódicos, formando um conjunto essencial para operações do cotidiano e avanços científicos.
Neste resumo, exploraremos a definição, propriedades e aplicações dos números racionais, destacando sua importância histórica e prática. Desde as civilizações antigas até os dias atuais, esses números têm sido uma ferramenta indispensável para medições, cálculos e o desenvolvimento de teorias matemáticas mais complexas.
Definição e Representação dos Números Racionais
Os números racionais, representados pelo símbolo ℚ, são todos aqueles que podem ser expressos na forma de fração a/b, onde:
- a (numerador) é um número inteiro;
- b (denominador) é um número inteiro diferente de zero (b ≠ 0).
Essa definição inclui:
- Números inteiros (ex.: 5 = 5/1);
- Frações próprias e impróprias (ex.: 3/4, 7/2);
- Decimais finitos (ex.: 0,75 = 3/4);
- Dízimas periódicas (ex.: 0,333… = 1/3).
Propriedades dos Números Racionais
Os números racionais possuem características importantes que facilitam operações matemáticas:
- Fechamento: A soma, subtração, multiplicação e divisão (exceto por zero) de dois racionais resulta em outro número racional.
- Comutatividade e Associatividade: Valem para adição e multiplicação (ex.: a + b = b + a).
- Elemento Neutro: 0 para adição (a + 0 = a) e 1 para multiplicação (a × 1 = a).
- Inverso Aditivo e Multiplicativo: Todo racional a/b tem um inverso aditivo (-a/b) e, se a ≠ 0, um inverso multiplicativo (b/a).
Operações com Números Racionais
As operações básicas seguem regras específicas:
- Adição/Subtração: Encontra-se o MMC dos denominadores para igualá-los antes de calcular.
- Multiplicação: Multiplicam-se numeradores e denominadores diretamente (a/b × c/d = ac/bd).
- Divisão: Inverte-se a segunda fração e multiplica-se (a/b ÷ c/d = a/b × d/c).
Essas propriedades e operações tornam os números racionais versáteis para resolver problemas do dia a dia, como divisão de quantidades e cálculos financeiros.
Aplicações dos Números Racionais
Os números racionais estão presentes em diversas áreas do conhecimento e situações cotidianas, demonstrando sua utilidade prática:
- Medições e Proporções: Usados em receitas culinárias, escalas de mapas e misturas químicas, onde quantidades precisam ser divididas ou combinadas com precisão.
- Economia e Finanças: Essenciais para calcular juros, porcentagens, descontos e divisão de gastos, como em contas compartilhadas.
- Engenharia e Construção: Empregados em projetos arquitetônicos para representar dimensões fracionadas (ex.: 1/2 polegada em tubulações).
- Estatística: Fundamentais para expressar probabilidades, médias e índices, como taxas de crescimento populacional.
Números Racionais vs. Irracionais
Embora os racionais cubram uma vasta gama de situações, existem números que não podem ser representados como frações, os irracionais (ex.: √2, π). A principal diferença está na representação decimal:
- Racionais: Decimais finitos ou infinitos periódicos (ex.: 0,5 ou 0,142857…).
- Irracionais: Decimais infinitos e não periódicos (ex.: π = 3,14159265…).
Juntos, racionais e irracionais formam o conjunto dos números reais, ampliando as possibilidades de representação matemática.
Curiosidades Históricas
O conceito de números racionais remonta a civilizações antigas, que já utilizavam frações para resolver problemas práticos:
- Egípcios: Usavam frações unitárias (com numerador 1) em sistemas de medição agrícola e construção de pirâmides.
- Gregos: Pitágoras e seus discípulos estudaram as proporções entre números inteiros, embora tenham descoberto os irracionais com √2.
- Índia e Mundo Árabe: Desenvolveram notações para frações e decimais, influenciando a matemática europeia durante a Idade Média.
Representação na Reta Numérica
Assim como os inteiros, os racionais podem ser dispostos em uma reta numérica, ocupando espaços densos entre os pontos:
- Entre dois números racionais, sempre existe outro racional (ex.: entre 1/2 e 3/4 está 5/8).
- Essa propriedade é conhecida como densidade, contrastando com a distribuição discreta dos inteiros.
Visualizar os racionais na reta ajuda a compreender sua ordenação
Conclusão
Os números racionais são pilares da matemática, permitindo representar quantidades fracionadas e decimais de forma precisa e versátil. Desde sua definição como frações até suas propriedades operacionais, eles facilitam cálculos cotidianos e avanços científicos. Suas aplicações — de finanças a engenharia — reforçam sua relevância prática, enquanto sua história revela uma evolução marcante no pensamento humano.
Dicas para Estudo
- Domine as operações básicas: Pratique adição, subtração, multiplicação e divisão de frações até torná-las intuitivas.
- Relacione com decimais: Converta frações em decimais e vice-versa para ampliar sua compreensão.
- Use a reta numérica: Visualizar os racionais ajuda a entender ordenação e densidade.
- Compare com irracionais: Diferencie representações decimais periódicas (racionais) das não periódicas (irracionais).
- Aplique em problemas reais: Resolva situações práticas, como ajuste de receitas ou cálculos de porcentagem, para fixar o conteúdo.
Com dedicação e prática, os números racionais se tornarão ferramentas naturais no seu repertório matemático, abrindo portas para temas mais complexos.